Dopo ogni alluvione, o altri disastri naturali, dobbiamo fare i conti non solo con fango e distruzione, ma anche con il senso di impotenza nei riguardi di una Natura che appare impredicibile. La domanda che nasce naturale è “Ma perché gli scienziati non riescono a dirci, con un opportuno anticipo, quando e come si verificheranno questi eventi?”.
Partiamo dall’inizio: i fenomeni meteorologici sono retti da leggi fisiche (fondamentalmente non dissimili da quelle che regolano il moto dei pianeti o la caduta di un grave), noi conosciamo queste leggi, che sono sostanzialmente le equazioni della fluidodinamica, basterebbe quindi, a partire dalle condizioni iniziali dell’atmosfera, che ora possono essere fornite da stazioni meteo e rilevamenti satellitari, calcolare, con qualche opportuno metodo numerico, e ovviamente un computer, l’evoluzione del sistema e quindi fare le previsioni. A prima vista questo approccio sembrerebbe fattibile senza particolari difficoltà, e in effetti anche un genio come von Neumann solo negli anni Cinquanta pensava che fosse possibile fare previsioni meteo a lungo termine in modo accurato, e addirittura controllare il clima. Purtroppo le cose sono decisamente più complicate di come credeva von Neumann, e questo per due complicazioni che possono dare grossi problemi:
- il nostro sistema potrebbe essere molto sensibile rispetto alle condizioni iniziali, se succede si ha quello che è indicato con il termine “effetto farfalla”,
- ci sono inevitabili approssimazioni nella descrizione dei vari processi fisici coinvolti nella descrizione matematica del
Facciamo un passo indietro. A volte si dice “precisione astronomica”, probabilmente per il fatto che gli astronomi sono in grado di dirci con grande anticipo quando ci sarà la prossima eclisse. Ma se gli eventi atmosferici e quelli astronomici sono retti dallo stesso tipo di leggi matematiche (in sostanza risalenti a Newton) perché i meteorologi spesso sbagliano e gli astronomi no? In realtà, come dimostrato dal grande matematico (ma anche fisico, filosofo e ingegnere) Henri Poincaré circa 150 anni fa, nel tentativo di risolvere il problema di tre corpi interagenti gravitazionalmente, alla fine non c’è affatto, almeno a livello concettuale, una differenza tra meteorologia e astronomia.
Poincaré capì che le difficoltà incontrate dai matematici che l’avevano preceduto nel tentativo di risolvere il problema dei tre corpi, sono dovute a un’importante proprietà intrinseca del sistema: aveva scoperto il caos. Lasciamo a lui la parola:
Una causa piccolissima che sfugge alla nostra attenzione determina un effetto considerevole che non possiamo mancare di vedere, e allora diciamo che l’effetto è dovuto al caso. […] Ma se pure accadesse che le leggi della natura non avessero più alcun segreto per noi, anche in questo caso potremmo conoscere la situazione iniziale solo approssimativamente… può accadere che piccole differenze nelle condizioni iniziali ne producano di grandissime nei fenomeni finali. Un piccolo errore nelle prime produce un errore enorme nei secondi. La previsione diventa impossibile e si ha un fenomeno fortuito.
Poincaré per primo comprese la possibilità dell’esistenza di moti molto complicati, che oggi chiamiamo caotici, in conseguenza dei quali una piccola incertezza sulla condizione iniziale cresce esponenzialmente e quindi non permette di fare previsioni su un tempo arbitrariamente lungo. Questa sensibile dipendenza dalle condizioni iniziali venne poi battezzata con il suggestivo nome di “effetto farfalla”.
Recentemente, in seguito a un romanzo cinese (Cixin Liu, Il problema dei tre corpi, Mondadori) e a una popolare serie di film di fantascienza ispirati al libro, il comportamento caotico dei sistemi astronomici è diventato popolare anche tra chi non ha mai sentito parlare di Poincaré.
Ora sappiamo che nelle previsioni meteo le difficoltà non nascono solo dal fatto che l’atmosfera è descritta da equazioni molto complesse in cui sono coinvolte moltissime variabili. Il meteorologo statunitense Edward Lorenz (uno dei pionieri del caos) negli anni Sessanta, studiando un modello molto semplificato per la circolazione atmosferica, mostrò in modo inequivocabile che anche un sistema con poche variabili può essere caotico. Quindi anche se (ipoteticamente) l’evoluzione dell’atmosfera fosse regolata da un sistema con poche variabili, ugualmente, in presenza di caos, non saremmo in grado di fare previsioni dopo un certo tempo; come effettivamente accade per il modello introdotto da Lorenz che ha solo tre variabili. Questo è quello che viene chiamato effetto farfalla.
Lorenz ha avuto l’importante ruolo di riscoprire il risultato di Poincaré che, pur noto ai matematici, aveva avuto uno scarso impatto nella comunità scientifica. È stato proprio Lorenz, negli anni Settanta, ad affermare che una farfalla che batte le ali in Brasile può provocare un tornado in Texas. Che cosa significa?
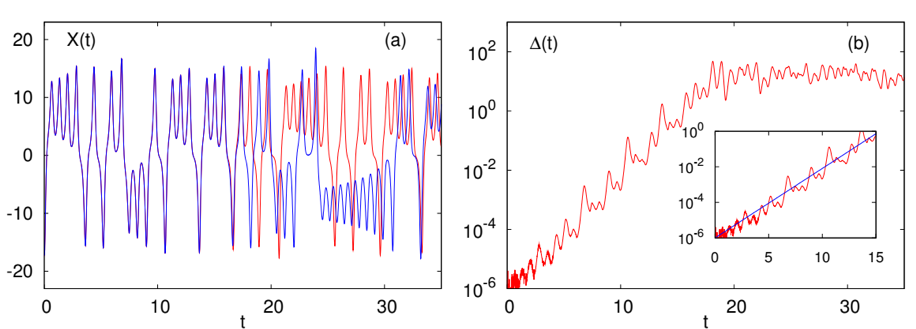
Figura 1: A sinistra l’evoluzione di una variabile del modello di Lorenz (tre equazioni differenziali) per due traiettorie inizialmente molto vicine, a destra la crescita esponenziale della distanza tra le due traiettorie. È ben evidente che non c’è speranza di fare previsioni a tempi lunghi.
Possiamo immaginare due situazioni iniziali dell’atmosfera quasi uguali, la differenza (piccola) è solo nella presenza di una farfalla che batte le ali, poiché la dinamica atmosferica è caotica, questa minuscola differenza sulla condizione iniziale ha come conseguenza che dopo un certo tempo (dell’ordine di un paio di settimane) le due evoluzioni potranno essere molto diverse, anche se non necessariamente con un tornado.
È importante sottolineare che il comportamento caotico trovato da Poincaré e Lorenz non è dovuto alla presenza di elementi aleatori: i sistemi studiati sono deterministici, cioè la condizione iniziale determina in modo univoco il sistema a ogni tempo. Nel caso di sistemi caotici il tempo oltre il quale è impossibile fare previsioni in modo accurato è determinato da un parametro chiamato esponente di Lyapunov. Questo tempo caratteristico è quello necessario per avere un aumento di un fattore e = 2,718 dell’errore iniziale: a causa della crescita esponenziale dopo qualche tempo caratteristico non abbiamo più la possibilità di una previsione accurata. L’aspetto fondamentale è che questo tempo caratteristico è una quantità intrinseca del sistema e non dipende dalla nostra bravura.
Ormai sappiamo che il caos è presente sia nel Sistema solare che in meteorologia, la differenza tra i due sistemi è nel valore del tempo caratteristico oltre il quale si manifesta l’instabilità: nel Sistema solare è qualche milione di anni, questo risultato è sicuramente interessante a livello matematico ma ci assicura che la “precisione astronomica” per le scale di tempo umano ha ancora senso.
La presenza dell’inevitabile incertezza dello stato presente (dovuta alla imprescindibile limitatezza delle reti di misura) e l’incompleta descrizione matematica di alcuni fenomeni fisici (ad esempio, la parametrizzazione della turbolenza presente su scale più piccole della risoluzione spaziale del modello usato) possono causare previsioni molto imprecise. Oltretutto, lo studio del caos deterministico ci ha insegnato anche che il tempo di predicibilità cambia con la condizione meteorologica: tipicamente, in concomitanza di eventi meteorologici estremi e disastrosi il tempo di predicibilità diventa molto breve.
Riassumiamo, con le parole di Robert May (uno dei pionieri del caos), la lezione più importante che Poincaré e Lorenz ci hanno insegnato: Non solo nel campo della ricerca ma anche nel mondo quotidiano della politica e dell’economia staremmo tutti di gran lunga meglio se più persone capissero che semplici sistemi non lineari non possiedono necessariamente semplici proprietà dinamiche.
Concludiamo con qualche osservazione generale per sfatare malintesi che purtroppo si possono trovare sulla stampa non specialistica, inclusi importanti quotidiani. A volte la scoperta del caos è presentata come qualcosa di negativo che, ponendo limiti alla possibilità di fare previsioni a lungo termine, intaccherebbe l’importanza della scienza. Per quanto a prima vista possa sembrare paradossale alcuni dei grandi risultati scientifici sono di tipo negativo, cioè sanciscono che alcune cose sono impossibili. Ad esempio, la relatività ci dice non si può superare la velocità della luce, e la meccanica quantistica stabilisce che non si possono determinare contemporaneamente con precisione arbitraria la posizione e la velocità di un elettrone. Analogamente la presenza del caos comporta l’impossibilità di previsioni su tempi arbitrariamente lunghi anche in sistemi di cui si conoscono perfettamente le equazioni di evoluzione. Questo risultato è solo apparentemente negativo, al contrario ha un risvolto decisamente pratico: ora sappiamo che, a volte, è inutile insistere nel sogno di previsioni arbitrariamente accurate.
Qualche volta, per illustrare la sensibile dipendenza dalle condizioni iniziali si ricorre all’esempio della tegola che cadendo dal tetto uccide uno sfortunato passante: se fosse passato poco primo o poco dopo le conseguenze sarebbero state molto diverse. Questo modo di presentare il caos, per quanto suggestivo, non rende l’essenza dei moti caotici: una tegola che cade non è una perturbazione piccola e in ogni caso avviene o non avviene una sola volta.
In un sistema caotico (come il modello di Lorenz e il problema dei tre corpi di Poincaré) ogni perturbazione, per quanto piccola, a qualunque tempo accada può avere un effetto catastrofico. Da questo punto di vista l’idea della farfalla che batte le ali e (forse) provoca un tornado racchiude l’idea del caos in modo decisamente più corretto della tegola che cade in testa al povero passante.
Angelo Vulpiani,
Università “La Sapienza”, Roma
Per saperne di più
- Cecconi, M. Cencini e F. Sylos Labini, “Si può prevedere il futuro?”, Le Scienze giugno 2003, pagina 32
- Gammaitoni e A.Vulpiani, Perché è difficile prevedere il futuro, Dedalo, 2019
- Galison, Gli orologi di Einstein, le mappe di Poincaré, Raffaello Cortina Editore, 2004
- Malvaldi e S. Marmi, Caos, Il Mulino, 2019
- H. Poincaré, Geometria e caso, Bollati Boringhieri, 1995
- Ruelle, Caso e caos, Bollati Boringhieri, 1992
- Vulpiani, Determinismo e caos, Carocci, 2004