La successione di Fibonacci
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, …
è una delle più famose successioni numeriche della storia della matematica. Il matematico medioevale Leonardo Pisano (Pisa, 1170-1242 ca), detto il Fibonacci, di cui la sequenza porta il nome, in realtà non si occupò dello studio di questi numeri che fecero solo una fugace comparsa in uno dei problemi contenuti nella sua famosa opera Liber Abaci: “Un uomo mette una coppia di conigli in un certo luogo interamente chiuso da un muro. Quante coppie di conigli sono generate a partire da questa coppia in un anno, se è nella natura dei conigli che ogni mese ogni coppia dia vita a un’altra coppia che nel secondo mese inizia anch’essa a riprodursi?”
È noto, inoltre, che Fibonacci non conoscesse nemmeno la proprietà fondamentale della successione di numeri che porta il suo nome: se Fn indica l’ n-esimo numero di Fibonacci, allora vale la relazione ricorsiva
Fn = Fn-1 + Fn-2
ovvero ogni numero a partire dal terzo è somma dei due numeri che lo precedono.
Sebbene i numeri di Fibonacci siano stati associati (e continueranno a esserlo) a Fibonacci e ai suoi conigli, essi apparvero molto tempo prima (200 a. C.) nell’opera Chandahsutra, un libro sulla metrica sanscrita del retore indiano Acharya Pingala. Nella prosodia sanscrita, l’unità di durata fonetica è detta mora (“ritardo”) mentre le unità di base sono sillabe con una mora (dette “brevi”) e sillabe con due more (dette “lunghe”). Denotate con B una sillaba breve e con L una sillaba lunga, il Chandahsutra riporta il numero di possibili schemi metrici aventi un dato numero di more: esiste un unico schema metrico costituito da una sola mora (B), ne esistono due costituiti da due more (BB, L), tre costituiti da tre more (BBB, LB, BL), cinque costituiti da quattro more (BBBB, LL, LBB, BLB, BLL), otto costituiti da cinque more (BBBBB, BBBL, BBLB, BLBB, LBBB, BLL, LBL, LLB) e così via a formare proprio la sequenza 1, 2, 3, 5, 8, 13, 21, 34, 55…
Per giustificare la conclusione appena fatta per via induttiva, si può osservare che ogni schema metrico costituito da un numero n di more termina o con una sillaba breve (B) o con una sillaba lunga (L) e quindi il numero sn di possibili schemi metrici di n more è la somma del numero di schemi metrici di n – 1 more e del numero di schemi metrici di n – 2 more, ovvero verifica la relazione ricorsiva del tipo sn = sn-1 + sn-2, che ha la stessa forma della relazione ricorsiva tra i numeri di Fibonacci.
Il ragionamento completo appena presentato si trova nel Chandonusasana, un altro trattato di prosodia sanscrita scritto intorno al 1150 dal matematico giaina Acharya Hemachandra. Non a caso, in India, i numeri di Fibonacci si chiamano numeri di Hemachandra. Un’applicazione non del tutto nota dei numeri di Fibonacci è legata alla determinazione del numero di tassellazioni di una scacchiera 1 x n, dove n è un numero naturale diverso da zero, tramite tessere del domino 1 x 1 e 2 x 1. In quanti modi è possibile farlo? Non è difficile riconoscere che il modello di questo problema è analogo a quello relativo agli schemi metrici indiani, in quanto la tassellazione della scacchiera può terminare con una tessera 1 x 1 oppure con una tessera 2 x 1. Di conseguenza, se tn indica il numero di modi di tassellare una scacchiera 1 x n, tn è proprio la somma del numero di modi di tassellare una scacchiera 1 x (n – 1) e del numero di modi di tassellare una scacchiera 1 x (n – 2), ovvero tn = tn-1 + tn-2.
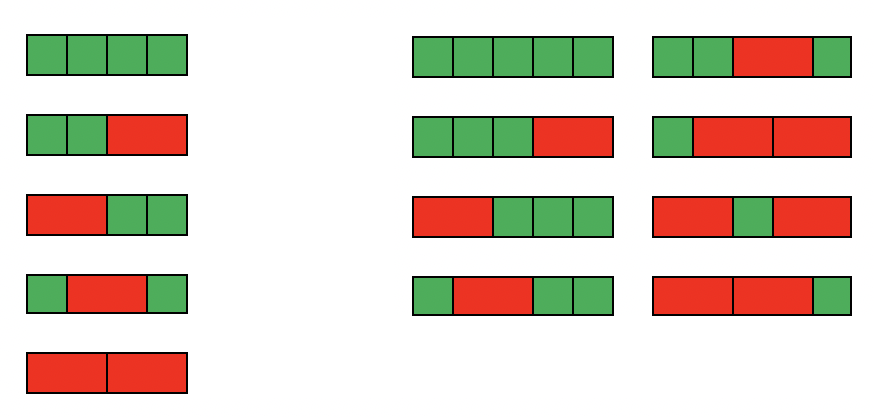
Dato che scacchiere 1 x 1 e 1 x 2 sono tassellabili rispettivamente in 1 e 2 modi, la relazione ricorsiva porta a t3 = 1 + 2 = 3, t4 = 2 + 3 = 5, t4 = 3 + 5 = 8, ovvero in generale tn = Fn+1. Le figure sottostanti mostrano tutte le tassellazioni di una scacchiera 4 x 1 e una scacchiera 5 x 1.
Una delle più note proprietà di cui gode la successione di Fibonacci è
F1 + F2 + F3 + … + Fn = Fn+2 – 1
ovvero la somma dei primi n numeri di Fibonacci è uguale all’ (n + 2)-esimo numero diminuito di 1. Ad esempio, la somma dei primi 6 numeri di Fibonacci 1 + 1 + 2 + 3 + 5 + 8, che fa 20, è uguale all’ottavo numero diminuito di 1, ovvero 21 – 1 =20.
Una delle dimostrazioni matematiche di questa relazione si basa sul principio di induzione, ma questo approccio non consente di averne una visione diversa da quella puramente algebrica. Daremo così una dimostrazione in termini di tassellazioni, mostrando l’idea (generale) nel caso particolare n = 6 e utilizzando la notazione riportata sopra. Procediamo nel modo seguente: dato che tn = Fn+1, la relazione da dimostrare diventa
1 + t1 + t2 + t3 + t4 + t5 = t7 – 1
ovvero
t1 + t2 + t3 + t4 + t5 = t7 – 2
Il membro di destra rappresenta il numero di tassellazioni di una scacchiera 1 x 7 eccetto 2 (al momento non sappiamo quali!). Si tratta di immaginare quali tassellazioni siano rappresentate dai cinque addendi t1, t2, t3, t4, t5.
Ciò è più semplice di quanto si potrebbe pensare. Infatti, t5 è il numero di tassellazioni della scacchiera 1 x 7 in cui le prime due caselle sono occupate da una tessera 2 x 1 (quindi le rimanenti cinque possono essere ricoperte in tutti i modi possibili con tessere 1 x 1 e 2 x 1). t4 è il numero di tassellazioni della scacchiera 1 x 7 in cui la seconda e la terza casella sono occupate da una tessera 2 x 1 (quindi, delle rimanenti, la prima deve necessariamente essere ricoperta da una tessera 1 x 1 mentre le rimanenti quattro possono essere ricoperte in tutti i modi possibili con tessere 1 x 1 e 2 x 1). Ragionando in maniera analoga, t3 è il numero di nuove tassellazioni della scacchiera 1 x 7 in cui la terza e la quarta casella sono occupate da una tessera 2 x 1, t2 è il numero di nuove tassellazioni in cui la quarta e la quinta casella sono occupate da una tessera 2 x 1 e t1 è il numero di nuove tassellazioni della scacchiera 1 x 7 in cui la sesta e la settima casella sono occupate da una tessera 2 x 1. La somma t1 + t2 + t3 + t4 + t5 dà tutte le tassellazioni della scacchiera tranne due: quella in cui la tessera 2 x 1 occupa la sesta e la settima casella mentre tutte le altre caselle sono coperte da tessere 1 x 1 e la tassellazione costituita interamente da tessere 1 x 1. Pertanto si ha t1 + t2 + t3 + t4 + t5 = t7 – 2.
Infine, esistono altri tipi di scacchiere, come quelle 2 x n, in cui il numero di tassellazioni tramite particolari tessere conducono ai numeri di Fibonacci. Il lettore saprebbe trovare un esempio?
Salvatore Damantino
Isis Malignani e Mathesis Udine
Per saperne di più
John J. Watkins, Number Theory. A Historical Approach, Princeton University Press, 2014
Piergiorgio Odifreddi, Numeri perversi, Le Scienze, febbraio 2017
Dal nostro catalogo: Teoria dei numeri, Aritmetica modulare, Problem solving in algebra e teoria dei numeri