Una parte considerevole della nostra esperienza quotidiana è vissuta in rapporto a materiali che si deformano applicando una piccola pressione: a volte tornano nella loro forma originale quando questa viene meno, altre volte restano deformati. Questi materiali reagiscono in modo elastico, come solidi, in alcune circostanze, e fluiscono, come liquidi, in altre. Collettivamente vengono chiamati “materia soffice”. La materia soffice include moltissimi esempi: da cibi a dentifrici, colle, gomme e paste industriali; dalla pelle ai muscoli, al cervello e così via. La maggior parte del nostro corpo è composta di materia soffice.
A livello microscopico, la materia soffice è composta di molecole che interagiscono debolmente tra loro. Stimoli di energia poco superiore a quella del moto termico possono far cambiare la forma e l’orientamento di queste molecole, e di conseguenza le proprietà del materiale. Tuttavia, le proprietà globali di questi materiali spesso non dipendono né dall’esatta natura chimica delle molecole né dalla loro esatta configurazione geometrica, in quanto viene continuamente modificata dal moto termico. Questo permette di costruire teorie molto generali, di scala, in cui le proprietà dei materiali vengono riportate a fenomeni microscopici emergenti, dovuti al fatto di avere un numero molto grande di molecole con certe proprietà generiche: quali, ad esempio, per i polimeri, la presenza di lunghe catene di unità chimiche che si ripetono, la loro densità, oltre al loro attrarsi o respingersi grazie a interazioni con il solvente.
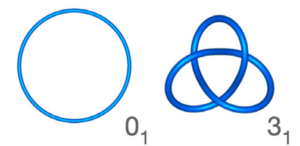
Il fatto che gli oggetti soffici abbiano infinite configurazioni geometriche, a livello microscopico, tra loro equivalenti al fine delle proprietà fisiche, rende necessario usare strumenti matematici che permettano di individuare quali famiglie di configurazioni risultino in comportamenti sostanzialmente diversi. Consideriamo come esempio un plasmide, cioè una molecola di DNA chiusa ad anello. Questi può assumere un continuo di configurazioni diverse, ma se le energie in gioco non sono troppo alte non può aprirsi. Nel chiudere la molecola però, se è abbastanza lunga, potremmo inserire un nodo, come quello che si fa alle scarpe. Una volta circolarizzata la molecola, il nodo non si può più sciogliere senza “tagliare il filo”. Anche in questo caso ci sono infinite conformazioni che contengono il nodo, ma tutte corrispondono a proprietà fisiche diverse rispetto a quelle dell’anello che non contiene il nodo. La branca della matematica che si occupa di caratterizzare questo tipo di proprietà che non dipendono da configurazioni geometriche precise è la topologia.
In topologia, gli oggetti di studio sono classi di equivalenza di diverse configurazioni geometriche, come i nodi dell’esempio precedente. Nello specifico, semplificando un po’, due configurazioni sono topologicamente equivalenti se esiste una trasformazione continua delle coordinate che mappi l’una nell’altra. Nel caso dell’anello semplice e dell’anello annodato questa non esiste: l’unica è tagliare il filo.
Ci sono moltissimi esempi di proprietà topologiche sia nei materiali soffici che in quelli biologici. Polimeri, come DNA e proteine, possono annodarsi; i plasmidi di DNA inoltre sono formati da due anelli intrecciati tra loro – i due filamenti che compongono la doppia elica – e il numero di intrecci, il linking number, è conservato; melt di polimeri anulari hanno proprietà radicalmente diverse rispetto a quelle di polimeri lineari; nei cristalli liquidi, le linee di disclinazione si possono annodare, e l’intero campo dato dall’orientazione delle molecole che li costituiscono può assumere strutture topologicamente diverse, dette solitoni.
Queste proprietà topologiche hanno da un lato conseguenze importanti per le proprietà fisiche e per il funzionamento biologico – o l’applicazione tecnologica – dei materiali soffici, e dall’altro possono venire usate per studiare meglio certi fenomeni fisici o biologici. La presenza di nodi nel DNA può portare a uno stallo della sua trascrizione; per evitarlo nelle cellule esistono degli enzimi chiamati topoisomerasi che “tagliano e ricuciono” il DNA sciogliendo eventuali nodi. Nelle proteine, la presenza di nodi impatta su alcune proprietà cinetiche, ma soprattutto deve essere tenuta in conto in una teoria che spieghi come queste prendano forma per raggiungere il loro stato tridimensionale nativo. Sempre in biologia, ci sono organismi, i tripanosomatidi, il cui DNA mitocondriale è formato da migliaia di plasmidi inanellati a formare una rete bidimensionale, il kinetoplasto. Questo è non solo un target importante per cure contro malattie quali la leishmaniosi e la malattia del sonno, ma è anche stato scelto come archetipo di materiale topologico bidimensionale, con esperimenti che dimostrano come si possano cambiare le sue proprietà reologiche se si aggiungono topoisomerasi in soluzione. Un altro esempio è fornito dei cristalli liquidi, in particolare nematici chirali, dove il packing di molecole vicine avviene con un angolo preferenziale. In questi materiali è possibile accoppiare la topologia del campo di orientamento a quella di campi elettromagnetici esterni, o si può controllare tramite l’inclusione di particelle colloidali.
Come si può intuire, la topologia è uno strumento utile a vari campi di ricerca che vanno dalla fisica, biologia di DNA e proteine, alle proprietà dei materiali polimerici, ai cristalli liquidi, a problemi di fisica dei campi, e molto altro. In Europa sono presenti molteplici gruppi di ricerca che lavorano su aspetti topologici della materia soffice e biologica. Nel 2017, assieme ad altri ricercatori, concepimmo l’idea di creare un network europeo per avvicinare i vari gruppi di ricerca europei che lavorano su problemi di natura topologica in biofisica e fisica della materia soffice, facilitando le interazioni tra esperti che usano strumenti simili in ambiti diversi. Da qui nacque la COST action Eutopia (European Topology Interdisciplinary Action), un network europeo formato da più di 150 scienziati di 29 paesi dell’Unione Europea, Sud-Africa, Stati uniti, Israele e Turchia.
La review “Topology in soft and biological matter” nasce all’interno del network Eutopia proprio per creare una sintesi tra ambiti diversi e facilitare gli scambi, aiutando la creazione di una nuova comunità scientifica. Il risultato è stato un articolo con 57 autori, i cui contributi sono stati discussi, integrati, riscritti assieme per produrre un manoscritto uniforme e di qualità. Questo approccio è piuttosto originale nell’ambito della fisica biologica e della materia soffice, dove in genere le scoperte sono prodotte da laboratori locali. Ancora oggi ci si aspetta infatti che rassegne di questo genere siano scritte da uno o due esperti, dotati di una visione approfondita di vari aspetti. Purtroppo, è ormai rarissimo trovare il tempo per approfondire varie discipline, per quanto legate da un filo comune, e probabilmente impossibile per una sola persona tenersi al pari con tutti gli sviluppi. Basti pensare che l’iper-specializzazione della scienza già un quarto di secolo fa dava spunto a grandi romanzi quali “Jurassic Park”. Allo stesso tempo però, è diventato molto più facile comunicare e coordinare gruppi di scienziati che lavorano in paesi e fusi orari diversi, anche grazie alle tecnologie introdotte per far fronte alla pandemia. Proprio questa capacità ci ha permesso di organizzarci e lavorare per produrre una review che fornisce un’ampia panoramica del ruolo della topologia nella materia soffice e biologica, partendo dagli strumenti base e arrivando agli sviluppi più recenti di un numero selezionato di argomenti. Scrivendo e confrontandoci è emerso chiaramente come tutti dessimo per scontati certi strumenti o assunti base del nostro campo di ricerca, senza neppure menzionarli nelle nostre discussioni, perché sono per noi assolutamente naturali. Ad esempio, la relazione tra condizioni al bordo e stati topologici era naturale per chi stava scrivendo la sezione di topologia in fisica dei campi, molto meno per chi si occupava di simulazioni di biopolimeri. Credo che alla fine la sintesi ci sia riuscita, e che siamo riusciti a costruire qualche ponte.
Luca Tubiana
Università di Trento