Una delle abilità a cui i matematici spesso fanno appello è quella di saper immaginare spazi nuovi.
Di solito in matematica si usa la parola spazio per trasmettere un’idea geometrica. Con l’espressione immaginare spazi mi riferisco all’atto di dare una lettura di tipo geometrico di una situazione che nulla ha, apparentemente, di geometrico, oppure all’atto di dare una lettura geometrica alternativa di oggetti geometrici. L’immaginare spazi permette ai matematici di approcciarsi a una situazione, fingendo di trovarsi davanti a una situazione famigliare quanto può esserlo un contesto geometrico. L’immaginare spazi svolge un ruolo fondamentale in molte aree della matematica. Prima di approfondire un esempio particolare, vorrei citare un altro paio di esempi importanti, anche se velocemente.
Il primo esempio è quello dell’algebra lineare. Protagonista di questa branca della geometria è il concetto di spazio vettoriale, che generalizza la struttura dei vettori (o dei punti) nel piano o nello spazio tridimensionale. Le funzioni lineari da uno spazio vettoriale all’insieme dei numeri reali formano, a loro volta, uno spazio vettoriale, detto spazio vettoriale duale. Questo ci permette di leggere queste funzioni come vettori o punti. Abbiamo quindi organizzato degli oggetti (queste particolari funzioni) in uno spazio adeguato che abbiamo saputo immaginare per esse.
Il secondo esempio è quello della meccanica analitica. In questo caso, se la configurazione di un sistema fisico immerso nel nostro spazio tridimensionale è determinata in modo univoco dal valore di \(n\) parametri, allora si possono utilizzare quei parametri come coordinate di un punto in uno spazio con \(n\) dimensioni; quel punto rappresenta la configurazione del sistema fisico e l’evoluzione di tale sistema corrisponde a una traiettoria del punto che lo rappresenta in questo nuovo spazio.
Passiamo ora al nostro esempio principale. Si tratta di un esempio che mi aveva colpito molto quando lo avevo incontrato da studente. Tra l’altro, esso riguarda degli oggetti molto amati e conosciuti, sia dai matematici che dagli appassionati: i frattali.
Innanzitutto dobbiamo parlare di un risultato celebre che ci sarà molto utile: il teorema delle contrazioni. Noto anche come teorema di punto fisso di Banach-Caccioppoli (1922-1930), è un teorema di estrema importanza. Per semplicità, mettiamoci nel piano euclideo che ben conosciamo. Una contrazione è una trasformazione del piano che fa diminuire la distanza tra ogni coppia di punti, in modo tale che esista un numero \(0<k<1\) per cui la distanza finale di ogni coppia di punti sia minore di \(k\) volte la distanza iniziale tra di essi. Un esempio di contrazione è una qualsiasi similitudine che abbia rapporto di similitudine minore di \(1\), per esempio quella che manda un punto del piano di coordinate \((x,y)\) nel punto di coordinate \((\frac{1}{2} y +1, \frac{1}{2}x +2)\).
Il teorema delle contrazioni afferma semplicemente che ogni contrazione ha un unico punto fisso, ovvero che esiste un unico punto che viene mandato in se stesso da essa. Nell’esempio che abbiamo considerato, il punto fisso si può trovare risolvendo le equazioni \(\frac{1}{2}x +1 =x \) e \(\frac{1}{2}y+2 =y \): è \((2,4)\).
In generale, tuttavia, il punto fisso non è così facile da individuare: serve un’idea diversa, che funzioni in ogni situazione. Quest’idea è quella di partire da un punto qualsiasi \((a,b)\) del piano, applicargli la trasformazione, e poi applicare la trasformazione alla trasformazione… e così via. Grazie al fatto che stiamo considerando una contrazione, quello che si ottiene è una successione di Cauchy (ovvero una successione tale che, per ogni numero piccolo a piacere \(\epsilon \), da un certo punto in poi ogni coppia di termini disti meno di \(\epsilon \)) e le successioni di Cauchy hanno sempre un limite. Questo limite è il punto fisso cercato come si può far vedere sfruttando le proprietà dei limiti e delle funzioni continue (come sono le contrazioni). Nel nostro caso, per esempio, partendo dal punto \((0,0)\), otterremmo la successione \((0,0),\, (1,2),\, (\frac{3}{2}, 3),\, (\frac{7} {4},\frac{7}{2}),\, (\frac{15}{8},\frac{15}{4}), \) …, \( (2-(\frac{1}{2})^{n +1}, 4-( \frac{1}{2})^{n})\), … i cui punti si avvicinano sempre di più al limite \((2,4)\). Per quanto riguarda l’unicità del punto fisso, possiamo semplicemente notare che se avessimo due punti fissi, la loro distanza non cambierebbe una volta applicata la contrazione, il che contraddice la definizione stessa di contrazione.
Benissimo: abbiamo spiegato questo teorema, ma perché ci interessa? Beh, innanzitutto si può riprodurre la stessa dimostrazione non solo nel caso di contrazioni del piano, ma nel contesto più ampio di contrazioni di uno spazio metrico completo non vuoto qualsiasi. Uno spazio metrico non è altro che un insieme non vuoto dotato di una distanza, ovvero di una funzione che associa a ogni coppia di elementi \(x\) e \(y\) dell’insieme un numero reale positivo, la loro distanza \(d(x,y)\), in modo tale che queste distanze soddisfino alcune proprietà fondamentali: \(d(x,y)\) deve essere \(0\) se e solo se \(x=y,\, d(x,y)=d(y,x)\) per ogni coppia di elementi \(x,\,y\) dell’insieme e, infine, la distanza \(d(x,y)\) deve essere minore o uguale a \(d(x,y)+d(y,z)\), per ogni terna di elementi \(x,\,y,\,z\) dell’insieme. Le tre richieste sono sensate e vengono incontro alla nostra idea informale di cosa significhi distanza. Il fatto interessante è che queste proprietà alla fine sono sufficienti a farci dimostrare il teorema delle contrazioni, se aggiungiamo a esse la cosiddetta completezza, ovvero la proprietà per cui ogni successione di Cauchy abbia un limite.
Veniamo quindi ai frattali: un frattale autosimile nel piano è un suo sottoinsieme non vuoto chiuso e limitato \(F\) per il quale esista una famiglia di similitudini \((S_i)_{i=1,…,n}\) con rapporti di similitudine minori di \(1\) tali che \( F \) è uguale all’unione degli insiemi che si ottengono applicando a esso stesso le similitudini \( (S_i) \). Di sicuro esistono frattali autosimili: i libri divulgativi ne sono pieni. Ma data una famiglia di similitudini \((S_i)_{i=1,…,n}\) ne esiste sempre uno rispetto a essa? E se ce n’è uno, ce ne possono essere altri? Domande naturali, direbbe un matematico. Le risposte sono sì e no, rispettivamente. Ma più che le risposte, ci interessa il perché delle risposte. E questo perché si basa sull’immaginare uno spazio nuovo, uno spazio strano, i cui punti non sono punti del piano, ma insiemi di punti del piano. Più precisamente, i punti del nuovo spazio sono i possibili candidati a essere frattali autosimili, cioè i sottoinsiemi del piano non vuoti, chiusi e limitati; tra di essi ci sono per esempio tutti i quadrati chiusi e tutti i cerchi chiusi del piano. Ma per fare dell’insieme di questi sottoinsiemi uno spazio dobbiamo legare in qualche modo i punti tra loro con una qualche nozione di tipo geometrico, in questo caso con una nozione di distanza. Si definisce quindi la distanza tra due punti del nuovo spazio, ovvero tra due insiemi non vuoti, chiusi e limitati \(A\) e \(B\), come il più piccolo numero reale \(r\) tale che “allargando” \(A\) di \(r\) si può “inglobare” \(B\) e “allargando” \(B\) di \(r\) si può “inglobare” \(A\). Per esempio, la distanza tra i due cerchi in figura è il massimo tra \(4\) e \(2\), ovvero \(4\).
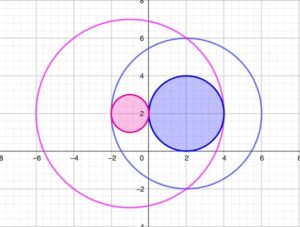
Questa distanza è detta distanza di Hausdorff, e trova molte altre applicazioni, anche al di fuori della matematica (per esempio, nel confronto e nel riconoscimento di proteine). Ora, la bella sorpresa è che il processo di applicare a ogni punto \(A\) del nuovo spazio le similitudini \(S_i\) e di unire i risultati è una trasformazione del nuovo spazio che è una contrazione! E il teorema delle contrazioni ci dà un unico punto fisso, che non è altro che il frattale autosimile che stavamo cercando… Questa dimostrazione si deve a John E. Hutchinson (1979).
Tra l’altro, la dimostrazione del teorema delle contrazioni ci dice anche come costruire il frattale: si parte da un qualsiasi insieme non vuoto, chiuso e limitato, si applicano le similitudini, e poi si applicano le similitudini al risultato e così via… Dopo un certo numero grande di passi, la nostra vista non sarebbe in grado di distinguere la differenza tra la figura che vediamo e il vero e proprio frattale. Questo, a fini “artistici”, è più che sufficiente, ed è stato sufficiente anche alla natura quando ha prodotto il broccolo romanesco.
Samuele Maschio
