Un contadino acquista un nastro colorato bianco e rosso che vuole fissare al suolo per segnalare il confine occidentale della sua proprietà, che è un segmento di retta lungo un chilometro. Per errore, egli acquista un nastro lungo un chilometro e un metro, ma se ne accorge solo nel momento in cui fissa il nastro al suolo alle due estremità e nota che non è teso. Per questo motivo a metà del confine decide di sollevare il nastro quanto basta per tenderlo dalle due parti. Quale animale potrà passare sotto il nastro sollevato e teso?
a) Una formica
b) Un topo
c) Un cane
d) Una giraffa
Il piccolo errore relativo commesso nell’acquisto del nastro ci suggerisce intuitivamente che le risposte corrette siano la a) e forse la b).
Ma analizziamo il problema con la matematica: possiamo usare il teorema di Pitagora. La lunghezza di mezzo segmento di confine è \(500\) metri. La lunghezza di mezza corda tesa è \(500,5\) metri. Essi sono rispettivamente un cateto e l’ipotenusa di un triangolo rettangolo. Quello che dobbiamo fare è calcolare la lunghezza dell’altro cateto: essa è
$$ \sqrt{ ((500,5m)^2-(500m)^2)} \simeq 22,36m. $$
Dunque sotto il filo teso può passare una giraffa… e forse anche quattro o cinque giraffe, se sanno stare una sopra l’altra come equilibriste.
Questo esempio dimostra che nonostante l’intuito sia un grande amico dell’essere umano e, in particolare, di chi fa matematica, a volte lo può trarre in inganno. Nell’immaginario collettivo il matematico è spesso descritto come una persona intuitiva che sa cogliere istantaneamente fatti profondi per altri ben lontani dall’essere evidenti. D’altra parte, chi fa matematica usa spesso espressioni come “Questo fatto è intuitivamente vero”. Ovviamente, la matematica non è fatta di sola intuizione. Le intuizioni forniscono idee le quali però devono passare il test del rigore, essere dimostrate valide, e non solo essere intuitivamente valide. Vorrei qui di seguito proporre al lettore qualche esempio significativo di fatti o concetti intuitivamente corretti, che si sono dimostrati rigorosamente sbagliati.
Vorrei iniziare questa piccola galleria, che è solo una piccola selezione dettata dai miei gusti personali, con un concetto che sembra apparentemente innocuo, perché gran parte di noi lo conosce fin dai primi anni di scuola: il concetto di insieme. Il concetto intuitivo che abbiamo di insieme è quello di estensione di una proprietà. Questo concetto intuitivo si esprime tramite due principi fondamentali, con i quali chiunque abbia affrontato gli insiemi alla scuola dell’obbligo sarà d’accordo:
- Due insiemi che hanno gli stessi elementi sono uguali.
- Per ogni proprietà esiste l’insieme degli oggetti che soddisfano tale proprietà.
Il principio 2 ci assicura, per esempio, che esiste l’insieme dei cani, dato che essere un cane è una proprietà. Siamo abituati da sempre ad usare il principio 2: esso è intuitivamente corretto.
Cosa succede però se come proprietà prendiamo questa?
Essere un insieme che non appartiene a se stesso.
Grazie al principio 2 esiste l’insieme \(W\) degli insiemi che non appartengono a se stessi. A questo punto è lecito porsi una domanda: \(W\) appartiene a \(W\)?
- Se \(W\) appartenesse a \(W\), allora non apparterrebbe a sé stesso.
- Se \(W\) non appartenesse a \(W\), allora apparterrebbe a sé stesso.
Abbiamo quindi una contraddizione. Qualcosa di intuitivamente corretto ci ha portato a una contraddizione… È quindi possibile che il principio 2 non sia poi così corretto…
Questo paradosso, scoperto da Russell nei primi anni del XX secolo, fu una scossa tellurica per le fondamenta della matematica e contribuì ad aprire una fase nota come Crisi dei Fondamenti che coinvolse numerosi matematici e filosofi i quali cercavano di risolvere il problema del sistema di base su cui fondare l’intero edificio matematico.
Il secondo esempio si colloca a cavallo tra numeri e insiemi: si tratta del teorema di Goodstein, un teorema controintuitivo, che riguarda alcune particolari successioni di numeri naturali. Si inizia con un numero naturale qualsiasi \(n\). Lo si scrive in base \(2\), scrivendo anche gli esponenti in base \(2\) e poi gli esponenti degli esponenti e così via… Tale notazione è detta notazione ereditaria in base \(2\) di \(n\). Per esempio, per \(n=24\),
$$ 24 = 2^4 +2^3 = 2^{2^2} + 2^{2^1} = 2^{2^{2^1}} + 2^{2^1+1}. $$
Dopo aver fatto questo si sostituisce ogni \(2\) con un \(3\) e si sottrae \(1\). Ad esempio nel caso in cui \$n=24\$, abbiamo il valore
$$ 3^{3^{3^1}} + 3^{3^1+1} – 1 = 7625597485067 .$$
Esprimiamo quindi il risultato in base \(3\) ereditaria, sostituiamo i \(3\) con dei \(4\) e sottraiamo \(1\).
Si continua così, ed eventualmente ci si ferma se si raggiunge lo \(0\). La successione di numeri ottenuta è nota come successione di Goodstein, perché fu studiata dal matematico Reuben Goodstein in un articolo del 1944. Nei casi in cui \(n=0,1,2,3\) la successione va a \(0\) dopo un numero molto piccolo di passi, mentre dal caso \(n=4\) in poi, si intuisce che essa comincia a crescere senza controllo. Per esempio, nel caso \(n=24\), il valore successivo a quello calcolato è dell’ordine di grandezza di \(10^{3^8}\) e nulla sembra suggerire che questo valore non aumenterà ancora al passo successivo enormemente e così via. Ciononostante, contro la nostra intuizione, Goodstein dimostrò che, qualsiasi sia il numero \(n\) di partenza, la successione prima o poi arriva a \(0\). Per farlo usò un argomento raffinato che richiedeva l’uso degli ordinali. L’idea è la generalizzazione di un’idea che si usa a volte per dimostrare che un qualche processo termina in un tempo finito: si associa ad ogni stato del processo un numero naturale e si verifica che mentre il processo va avanti tali numeri naturali decrescono strettamente; dato che i numeri naturali non possono decrescere per sempre, il processo terminerà. L’idea di Goodstein è simile, ma utilizza gli ordinali al posto dei numeri naturali. Il risultato di Goodstein è peraltro interessante perché è uno di quei risultati sui numeri naturali che non possono essere dimostrati nella teoria del primo ordine dell’aritmetica di Peano, ma che sono dimostrabili nella teoria degli insiemi.
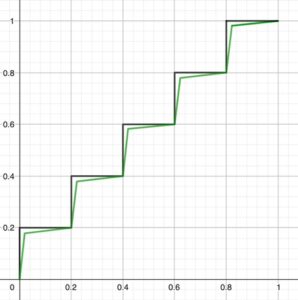
Il terzo esempio viene dall’analisi. Consideriamo le funzioni continue \(f\) dall’intervallo \([0,1]\) all’intervallo \([0,1]\) non decrescenti tali che \(f(0)=0\) e \(f(1)=1\). Quanto può essere lunga la curva del loro grafico? Beh, intuitivamente la lunghezza minima è \( \sqrt{2}\), ed è effettivamente così: basta considerare la funzione identità. E per la lunghezza massima? Esiste una lunghezza massima? Beh, se il grafico di una funzione potesse essere anche verticale diremmo che la lunghezza massima è \(2\) (ogni scalinata che porta da \( (0,0) \) a \( (1,1) \) ha questa lunghezza), ma, intuitivamente, sebbene tale lunghezza possa essere avvicinata a piacere dal grafico di una funzione del nostro tipo, essa non può mai essere uguagliata. Possiamo infatti spingere un po’ alcuni vertici di una scalinata in modo da trasformarla nel grafico di una funzione non decrescente continua e ottenere per esso una lunghezza vicina quanto vogliamo a 2, come mostrato nella prima figura; tuttavia sembra proprio che il valore \(2\) non possa essere mai raggiunto… Sembra, ma non è così. Una funzione introdotta da Georg Cantor nel 1844 ha infatti le proprietà desiderate e il suo grafico è una curva di lunghezza \(2\). La sua costruzione può essere descritta in diversi modi. Una possibilità è questa: si divide l’intervallo \( [0,1]\) in 3 intervalli uguali e sui punti dell’intervallo centrale il valore della funzione è posto uguale a \( \frac{1}{2} \). Si divide ora ognuno dei due intervalli rimanenti in 3 parti e si assegna ai punti della parte centrale dell’intervallo di sinistra il valore \( \frac{1}{4} \) e ai punti della parte centrale dell’intervallo di destra il valore \( \frac{3}{4} \). Si continua così, ogni volta dividendo gli intervalli rimanenti in 3 parti e assegnando ai punti delle parti centrali valori del tipo \( \frac{k}{2^n} \) con \(n\) che aumenta di passo in passo e \(k\) dispari che è scelto in modo da garantire la monotonia della funzione. Iterando il processo all’infinito, si assegna il valore della funzione sui punti di un sottoinsieme denso di \( [0,1]\). Infine si completa la definizione della funzione di Cantor imponendo la sua monotonia e si ottiene la sua continuità.
Il quarto esempio è famosissimo, si tratta del celebre problema di Monty Hall: ci sono tre porte dietro le quali si celano due capre e una magnifica automobile sportiva. Ci viene chiesto di scegliere una porta: vinceremo ciò che si trova dietro. Ovviamente, puntiamo all’automobile sportiva. Una volta scelta la porta, il conduttore del gioco apre una delle altre due porte mostrandoci che dietro ad essa c’è una capra. A questo punto ci offre la possibilità di cambiare la nostra scelta. Conviene cambiare o no? Intuitivamente ci sembra che la probabilità di avere dietro alla nostra porta una bella automobile sia \( \frac{1}{2} \), quindi cambiare non sembra fare differenza: la probabilità di vittoria intuitivamente è la stessa nei due casi. Ebbene, l’intuizione ci inganna: conviene cambiare, avremmo i \( \frac{2}{3} \) di probabilità di vittoria! Se non ci crediamo, possiamo scriverci per bene su un foglio i casi e calcolare la probabilità con la bella formula della probabilità classica, casi favorevoli/casi possibili, oppure possiamo fare un po’ di prove e contare i successi per modificare la nostra intuizione. Possiamo usare disegni di capre e di auto sportive, per fortuna non serve che ne compriamo di vere per l’esperimento.
Samuele Maschio